Toycoin Part 5: Blocks
Note: the toycoin series of posts is for learning / illustrative purposes only; no part of it should be considered secure or useful for real-world purposes.
With some underlying requiremnts covered in the previous posts, we get to blocks. Following the - Nakamoto paper, a block consists of a header and some transactions:
Transactions = List[transaction.Transaction]
class BlockHeader(TypedDict):
timestamp: bytes
previous_hash: hash.Hash
nonce: bytes
merkle_root: hash.Hash
this_hash: hash.Hash
class Block(TypedDict):
header: BlockHeader
txns: Transactions
BlockChain = List[Block]
As transactions are broadcast to the blockchain network, full nodes will collect them, validate them, and with some consensus mechanism (proof of work here), append new blocks to the blockchain.
As more blocks are added to the blockchain, it becomes incresingly unlikely that a transaction from a bad actor involved double spending.
Building on teh transaction example from an earlier post, we have a information flow that looks roughly like this:
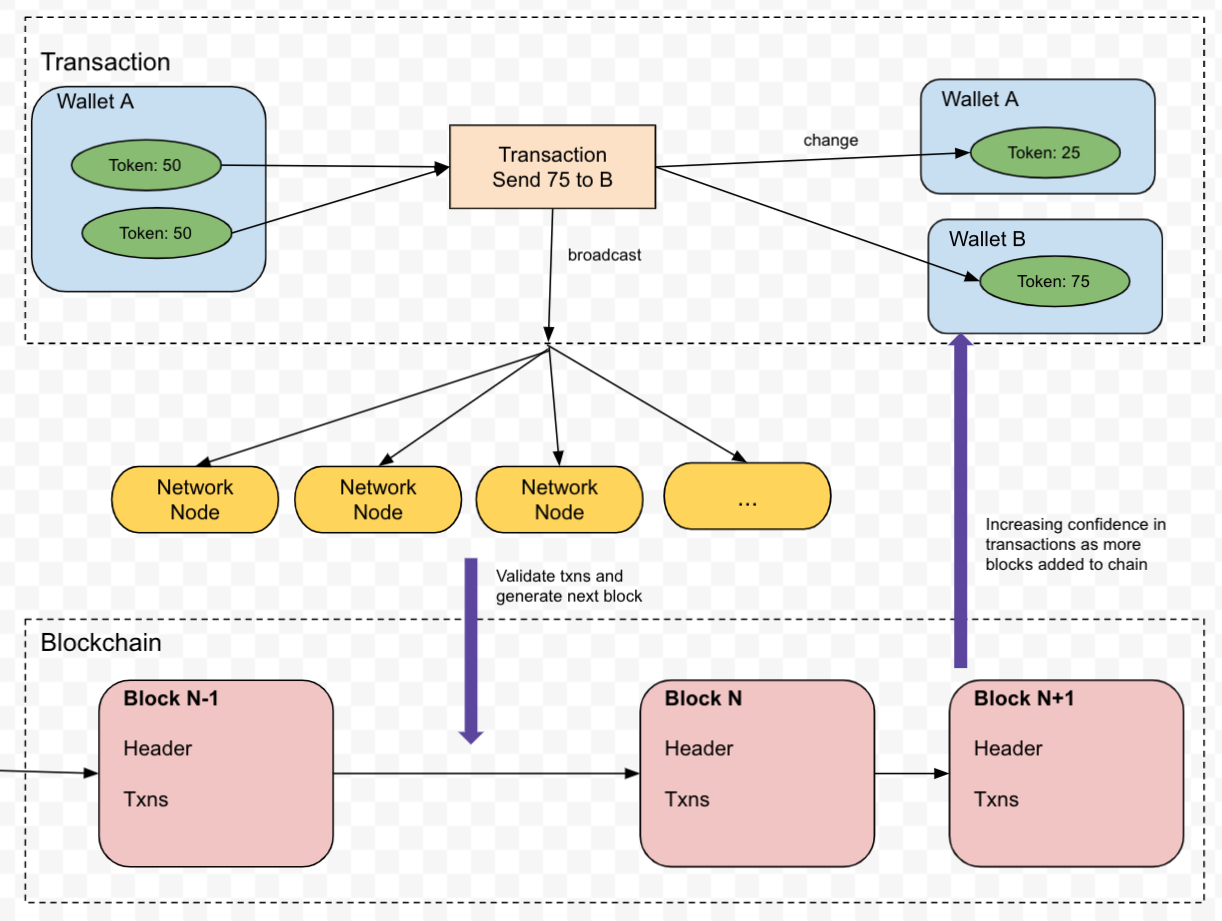
Generating Blocks
To generate a block, we supply the previous block hash, transactions, and the current proof-of-work difficulty. the function then returns a generated block (if possible) and any “remainder” transactions that weren’t processed. Some notes:
- this assumes at least one transaction is required to generate a block
- to keep the function pure, the state of the blockchain is represented in the inputs
previous_hashanddifficulty; a calling client could pass in something arbitrary, but then no honest node following the blockchain validation protocol would accept it as a valid block
def gen_block(previous_hash: hash.Hash,
txns: Transactions,
difficulty: int
) -> Tuple[Optional[Block], Transactions]:
"""Attempt to generate a block from transactions.
Return a block (or None if failure), and remainder transactions.
"""
if not txns:
return None, []
txns_, rest = txns[:BLOCK_TXNS], txns[BLOCK_TXNS:]
tree = gen_merkle(txns_)
header = proof_of_work(previous_hash, tree.label, difficulty)
block : Block = {'header': header,
'txns': txns_}
return block, rest
Proof of Work
Though it seems that proof-of-stake has greater benefits and will be favored by many blockchains going forward, the consensus protocol for toycoin follows Nakamoto’s paper (Section 4 Proof-of-Work).
In short: perform some computation – in this case, find a hash with an increasing number of leading zero bits (or bytes). Honest nodes will work to extent valid blockchains, makingi t increasingly (exponentially) harder for attackers to double spend coins, unless they control the majority (51%) of computational power on the network.
The Nakamoto paper contemplates a self-adjusting level of difficulty for the proof-of-work, based on network throughput. The toycoin implementation is naive and far simpler:
def next_difficulty(length: int) -> int:
"""Determine difficulty of next block, given length of current chain."""
return 1 if length < 1 else 1 + int(math.log2(length))
def proof_of_work(p: hash.Hash,
root: hash.Hash,
difficulty: int
) -> BlockHeader:
"""Naive POW solver."""
now = utils.int_to_bytes(utils.timestamp())
nonce = 0
h = b''
while not solved(h, difficulty):
nonce += 1
h = hash.hash(now + p + utils.int_to_bytes(nonce) + root)
return {'timestamp': now,
'previous_hash': p,
'nonce': utils.int_to_bytes(nonce),
'merkle_root': root,
'this_hash': h}
def solved(h: hash.Hash, n: int) -> bool:
"""Check if first n bytes are zeros."""
return h[:n] == bytes(n)
If an incentive for producing the proof-of-work (“mining”) is to be included in toycoin, it could presumably be handled later by the node / network procol.
Validation
Though in most cases network nodes would probably want to minimize the need validate the entire blockchain (instead validating blocks incrementally), such a function looks like the following, where check for:
- valid “chaining” from one block to then next, i.e. each block incorporates the previous block’s hash
- valid individual blocks, e.g. the hash is valid and is of the correct difficulty
`def valid_blockchain(chain: BlockChain) -> bool:
"""Check validity of blockchain."""
pairs = zip(chain[1:], chain)
v1 = all(valid_hash_pair(b1, b0) for b1, b0 in pairs)
v2 = all(valid_block(block, next_difficulty(i))
for i, block in enumerate(chain))
v3 = chain[0]['header']['previous_hash'] == GENESIS
return v1 and v2 and v3
There is also a check that the first block has a magic genesis hash. Maybe that doesn’t add much.
Testing
Similar to transactions and wallets, the interesting tests for block involve mocking a scenario and generating a bunch of transactions and blocks, performing various validity checks at each step. It is tedious to read and long so is omitted here, but see the source.
Wrapping Up
At this point, the pure, side-effect free part of toycoin feels mostly done. There are probably still a few fundamentals missing, but they should be revealed upon trying to implement and test the node logic and networking protocols.
I do feel like I have a stronger understanding of blockchain basics… but on the other hand, the point of the blockchain is the decentralized, peer-to-peer network, so maybe I’ve not understood much at all yet.
I’ve only done some very basic network exercises, so the technical learning curve will probably be a bit steeper. Part of the original goal was also to visualize the blockchain activity, for which I’d like to use Elm. That means… using websockets or SSE to send network events to Elm via Javascript ports?