Squarified Treemaps (in Elm)
A squariifed treemap is a treemap that tries to minimize the aspect ratio of its rectangles, i.e. tries to make things as square as possible.
It’s perhaps most commonly used in a heatmap, like so:
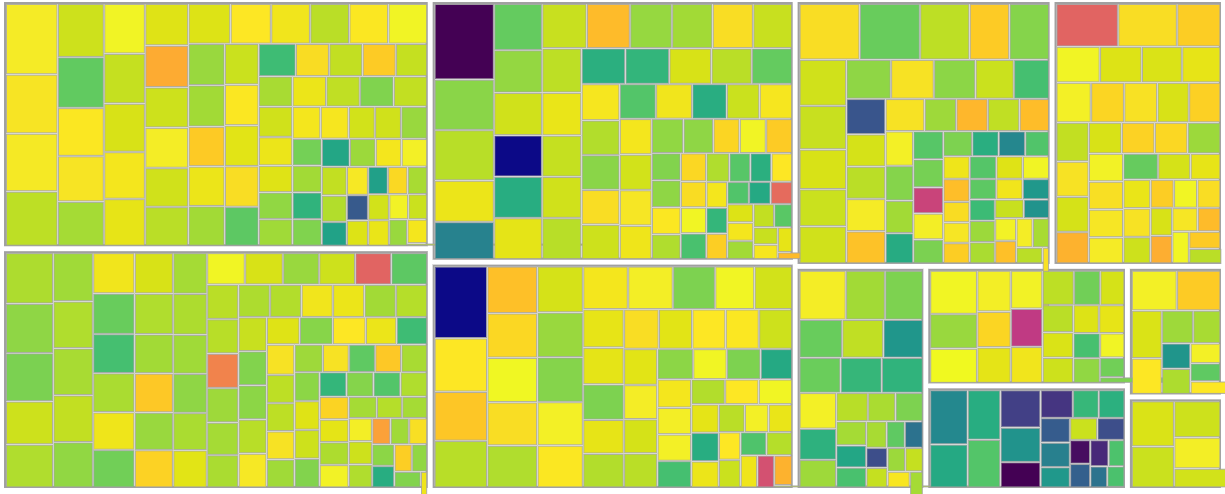
Finding the optimal (as square as possible) squarified treemap is an NP-hard problem, it would appear, but there’s a sinmple, greedy heuristic described in this paper that appears to achieve good results. An implementation in Elm follows.
Partition
Given a list of areas and a rectangle to fill, we want to partition the rectangle according to the list of areas (or “cells”). For convenience, the input cells are represented with the extensible record type alias HasArea a = { a | area : Float }, which just requires area to be in the record.
The paper uses the simple abstraction of a row to group cells together, where row can be subdivided either vertically or horizontally.
partition can be written as a fold over the input areas, where the below implementation has some additional code to work with List.Nonempty, imported as NE.
partition : Dimensions -> NE.Nonempty (HasArea a) -> NE.Nonempty (Row a)
partition dims areas =
NE.tail areas
|> List.foldl partitionHelper ( dims, NE.fromElement (NE.head areas), [] )
|> (\( _, row, rows ) ->
NE.Nonempty row rows
|> NE.map NE.reverse
|> NE.reverse
)
The fold function implements the paper’s pseudocode almost directly (note that the paper contains a typo in the direction of the comparison operator of the if clause, which the authors know about). The main idea is to greedily add another cell to the current row, so long as the row’s worst aspect ratio does not worsen.
type alias PartitionAcc a =
( Dimensions, Row a, List (Row a) )
partitionHelper : HasArea a -> PartitionAcc a -> PartitionAcc a
partitionHelper area ( dims, row, rows ) =
let
w =
Tuple.first <| sizeOrdered dims
in
if worst row w >= worst (NE.cons area row) w then
( dims, NE.cons area row, rows )
else
( updateDims dims row, NE.fromElement area, row :: rows )
There is some housekeeping required to update the working dimensions as new rows are added. (See implementations of updateDims and worstt in the full code).
We can test partition with the example from the paper:
> import DataGrid.Internal.SquarifiedTreemap as ST
> import List.Nonempty as NE
>
> areas = NE.Nonempty 6 [6, 4, 3, 2, 2, 1] |> NE.map (\a -> { area = a })
>
> ST.partition { x = 6, y = 4 } areas
Nonempty
( Nonempty { area = 6 } [{ area = 6 }] )
[ Nonempty { area = 4 } [{ area = 3 }]
, Nonempty { area = 2 } []
, Nonempty { area = 2 } []
, Nonempty { area = 1 } []
]
: NE.Nonempty (ST.Row {})
Because the algorithm always follows the shorter lenght of the remaining subrectangle, the above minimal representation of the partition result is all that’s needed to render the treemap.
Squarified Treemap
Given partition results, generating renderable cells (containing subrectangle x, y, width, and height information) is a matter of another fold, or, in the below, using mapAccumlL from Haskell to preserve the non-emptiness.
type alias SquarifiedTreemap a =
NE.Nonempty (Cell a)
type alias Cell a =
{ x : Float
, y : Float
, w : Float
, h : Float
, cell : HasArea a
}
type alias Origin =
{ x : Float
, y : Float
}
makeTreemap : Dimensions -> NE.Nonempty (HasArea a) -> SquarifiedTreemap a
makeTreemap dims areas =
partition dims areas
|> Utils.neMapAccumL rowToCells ( { x = 0, y = 0 }, dims )
|> Tuple.first
|> NE.concat
Since we now need the x and y for each cell, we need to track the current origin in addition to the current remaining subrectangle dimensions. The origin is shifted each time a row is completed (note that unlike the example in the paper, the origin is always increasing in this implementation).
updateOriginAndDims : Origin -> Dimensions -> Row a -> ( Origin, Dimensions )
updateOriginAndDims origin dims row =
let
dims_ =
updateDims dims row
origin_ =
{ x = origin.x + dims.x - dims_.x
, y = origin.y + dims.y - dims_.y
}
in
( origin_, dims_ )
The rowToCells function is another fold that threads the origin and dimensions through the current row to draw each cell.
rowToCells : Row a -> ( Origin, Dimensions ) -> ( NE.Nonempty (Cell a), ( Origin, Dimensions ) )
rowToCells row ( origin, dims ) =
let
( origin_, dims_ ) =
updateOriginAndDims origin dims row
delta =
{ x = dims.x - dims_.x
, y = dims.y - dims_.y
}
cells =
Utils.neMapAccumL rowToCellsHelper ( origin, delta ) row |> Tuple.first
in
( cells, ( origin_, dims_ ) )
Running makeTreemap on the same input as above, we get a list of cells that are ready to render:
> ST.makeTreemap { x = 4, y = 6 } areas
Nonempty
{ cell = { area = 6 }, h = 3, w = 2, x = 0, y = 0 }
[ { cell = { area = 6 }, h = 3, w = 2, x = 2, y = 0 }
, { cell = { area = 4 }, h = 1.7142857142857142, w = 2.3333333333333335, x = 0, y = 3 }
, { cell = { area = 3 }, h = 1.2857142857142856, w = 2.3333333333333335, x = 0, y = 4.714285714285714 }
, { cell = { area = 2 }, h = 1.2000000000000002, w = 1.6666666666666665, x = 2.3333333333333335, y = 3 }
, { cell = { area = 2 }, h = 1.2000000000000002, w = 1.6666666666666665, x = 2.3333333333333335, y = 4.2 }
, { cell = { area = 1 }, h = 0.5999999999999996, w = 1.6666666666666676, x = 2.3333333333333335, y = 5.4 }]
: ST.SquarifiedTreemap {}