Toycoin Part 2: Merkle Trees
Note: the toycoin series of posts is for learning / illustrative purposes only; no part of it should be considered secure or useful for real-world purposes.
Merkle trees are trees in which all data (or hashes thereof) reside in leaf nodes, and the interior nodes contain hashes of their children. The typical implementation is in the form of a binary tree.
The inclusion of Merkle trees in blockchains allow for simplified verification of transactions by network participants that are not running “full” nodes. This is described briefly in Section 8 of Nakamoto’s paper. My limited understanding of how such a simplfiied verification could be implemented is:
-
the participant queries the network until it’s reasonably certain it’s obtained the longest blockchain
-
the participant asks a full node for the block header of the block containing a transaction to be verified (which includes the Merkle root of the tree of transactions in that block), along with the path of hashes from the transaction in question to the root
-
if the node provides a valid path of hashes (i.e. terminating in the Merkle root contained in the block header), the transaction is assumed to be valid, since the block header has been accepted by the network (assuming there are subsequent blocks on the blockchain)
Interface
What interface should a Merkle tree provide? It seems like a basic implementation should feature something along the lines of:
def insert(tree: MerkleTree, leaf: Hash) -> MerkleTree
def from_list(nodes: List[Hash]) -> MekleTree
def valid(tree: MerkleTree) -> bool
def contains(tree: MerkleTree, leaf: Hash) -> HashPath
… where insert and from_list are constructors, while valid and contains are verification functions.
-
validis imagined to be a validation of the entire tree (i.e. verifying all hashes) -
containsis imagined to be a validation of an individual leaf, which returns the path of hahes from the leaf to root, if such a valid path exists, or nothing otherwise (say, an empty path). Returning the path is ,aybe less obvious than, say, a simplebool, but it’s the proof required for verifying the Merkle root stored in blockchain headers.
Implementation Considerations
What are some desirable properties of a Merkle tree?
Like many (most?) kinds of trees, the tree should as balanced as possible – or alternatively, of minimal height. This ensures optimal, logarithmic traversals from root to leaves.
Maintaining balance can be tricky, but that’s usually due to rebalancing algorithms that preserve some order in the tree. With Merkle trees, the main goal is to verify existence and validitiy, rather than to maintain some invariant order. (In fact, tt would presumably be diffuicult to maintain any kind of order if using a secure hashing algorithm.)
So we can try a simple imeplementation like right-most insertion:
-
if subtrees are not fully balanced, push new node down to the right-most leaf, then update hashes back up to the root
-
otherwise, start a new branch to the right (from the root downwards)
This also has the benefit of minimizing the number of hashes that need to be recomputed, since insertion does not alter existing hashes other than the root (although it may insert a small number of new interior nodes).
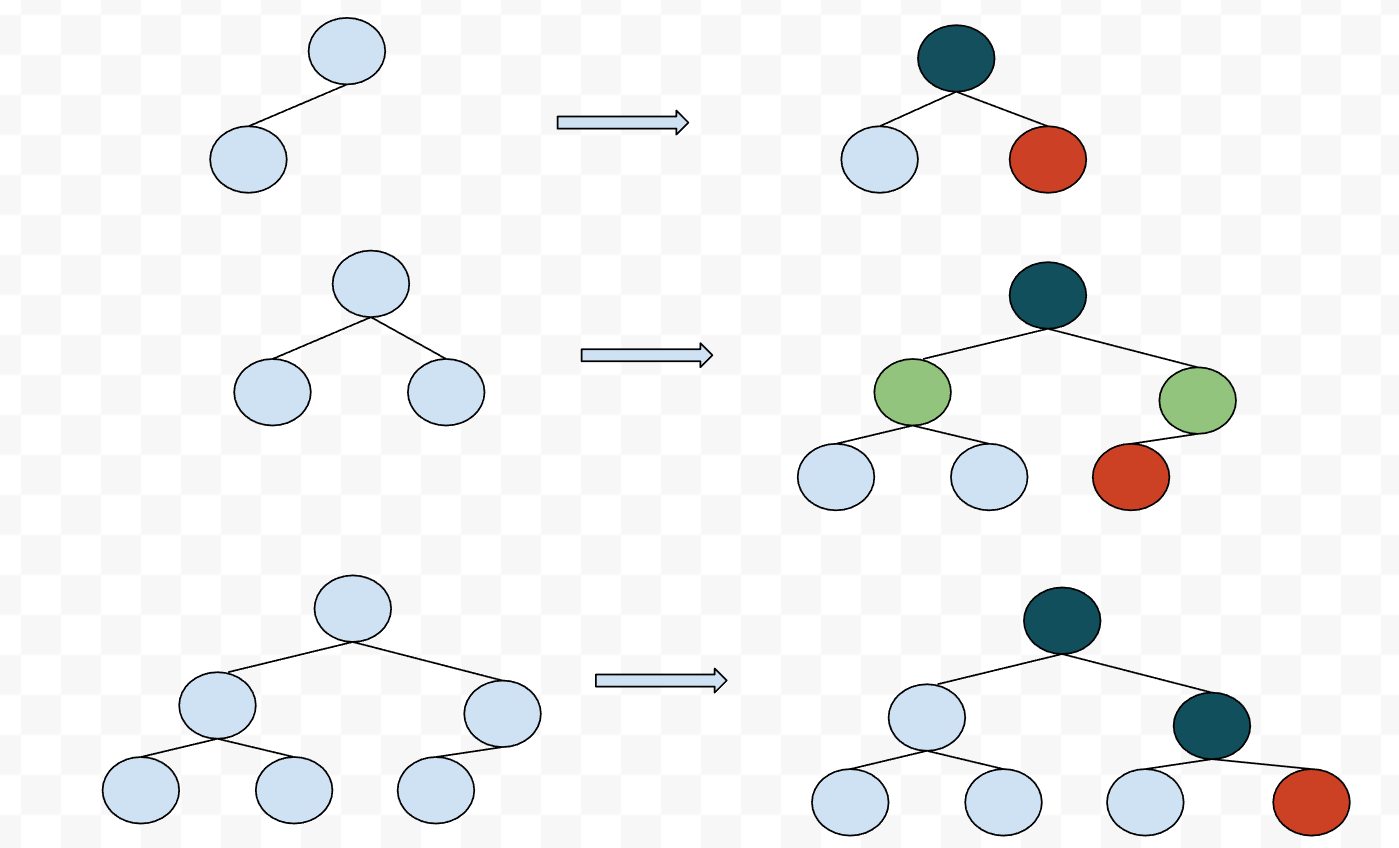
In the above:
- brown = newly inserted node
- dark green = existing interior node updated
- light green = new interrior node added
Implementation
A typical recursive implementation of a tree type looks something like:
type MerkleTree
= Leaf Hash
| Node MerkleTree Hash MerkleTree
In Python, without type constructors, I ended up with:
class MerkleTree:
"""Merkle hash tree.
Initialize with from_singleton() and from_list() functions.
"""
def __init__(self,
label: Hash,
left: Optional['MerkleTree'] = None,
right: Optional['MerkleTree'] = None
):
self.label = label
self.left = left
self.right = right
self.size = self.init_size(left, right)
def init_size(self,
left: Optional['MerkleTree'] = None,
right: Optional['MerkleTree'] = None
) -> int:
"""Helper for initializing size."""
if left is not None and right is not None:
size = left.size + right.size + 1
elif left is not None:
size = left.size + 1
else:
size = 1
return size
… so, in lieu of type constructors, leaf nodes are implciitly defined as trees with None children. Accordingly, we can define a simple helper function:
def is_leaf(tree: MerkleTree) -> bool:
"""Return True if given tree is a leaf node."""
return tree.left is None and tree.right is None
A few noteworthy points from mypy type-checking perspective:
- the quotes in
Optional['MerkleTree']is needed for annotating forward-referencing types - for
Optionaltypes,mypyrequires explicit narrowing (likeassert x is not None,if x is not None); currently, these cannot be written as one-liners, so it’s not possible to writeinit_sizeas a singlereturnexpression
Insertion follows the above logic of right-most insertion:
def insert(self, leaf: Hash):
"""Recurse insertion."""
# base cases
if self.left is None:
self.left = MerkleTree(b'\x00' + leaf)
self.update()
elif self.right is None:
self.right = MerkleTree(b'\x00' + leaf)
self.update()
elif self.left.size == self.right.size:
self.left = MerkleTree(self.label, self.left, self.right)
self.right = from_singleton(leaf)
self.update()
# recursive case
else:
self.right.insert(leaf)
self.update()
def update(self):
"""Update hash and size of interior node."""
assert self.left is not None
if self.right is None:
labels = self.left.label
size_ = self.left.size
else:
labels = self.left.label + self.right.label
size_ = self.left.size + self.right.size
self.label = b'\x01' + hash.hash(labels)
self.size = 1 + size_
In short, either insert the leaf to an empty spot, or expand the tree right-ward and insert the leaf, or recursively call insert on the right branch. update takes care of the housekeeping for size and interior hash updates.
Explicit pattern matching would probably be a bit more clear for handling the Optional types, but Python doesn’t have such syntax (yet).
Note that the implementation appends \x00 and \x01 bytes to leaf and interior nodes, respectively, to protect against second preimage attacks – discussed further below.
Construction
Constructors are provided as separate functions, though maybe it’s a bit awkward that initializing a MerkleTree instance isn’t the same as from_singleton. Note that a singleton node is still hashed by an interior node (the root).
def from_singleton(leaf: Hash) -> MerkleTree:
"""Create singleton Merkle tree, with root and one leaf."""
leaf_node = MerkleTree(b'\x00' + leaf)
root = MerkleTree(b'', leaf_node)
root.update()
return root
def from_list(leaves: List[Hash]) -> Optional[MerkleTree]:
"""Create Merkle tree from one or more nodes."""
if not leaves:
return None
head, tail = leaves[0], leaves[1:]
t = from_singleton(head)
for leaf in tail:
t.insert(leaf)
return t
Validation
The full implementation of the validation functions is omitted here, but can be found in the source.
The type signatures previously considered work fine, with some additional type aliases for clarity. A worked example follows below.
MaybeLeft = Optional[Hash]
MaybeRight = Optional[Hash]
HashTriple = Tuple[Hash, MaybeLeft, MaybeRight]
HashPath = List[HashTriple]
def valid(tree: MerkleTree) -> bool
def contains(tree: MerkleTree, leaf: Hash) -> HashPath
Example
Construction
For clarity of example, we’ll construct a tree without hashing the leaf nodes. The labels / hashes are encoded as hex for printing.
Create a singleton node tree:
In [1]: from toycoin import hash, merkle
In [6]: t = merkle.from_singleton(b'0')
In [7]: merkle.show(t)
-- Level 1 | Size 2 | Label: 8f0754f174e2f56b90deef3fb910f0ce33ba432dfe9b43b4f6bef70b0b32f716f331e7236f45a66bc09a26246ac0c37f13a95cd5f5f46ab72ed04dbfd2973cc3
---- Level 2 | Size 1 | Label: 30
Inserting a second node, we see that it fills the previously empty right leaf:
In [8]: t.insert(b'1')
In [9]: merkle.show(t)
-- Level 1 | Size 3 | Label: 069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e13316552bd08
---- Level 2 | Size 1 | Label: 30
---- Level 2 | Size 1 | Label: 31
As we insert a third and fourth node, we see that a new branch is created to the right, as expected.
In [10]: t.insert(b'2')
In [12]: t.insert(b'3')
In [13]: merkle.show(t)
-- Level 1 | Size 7 | Label: 8dc28b40624872b5ef939e482f3ab934e30c074422ac38b81c6fffe1394571d648dba783236d6d69b8ea472121ea8f35616a8926ddcdb565c6e0b1c60852cce6
---- Level 2 | Size 3 | Label: 069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e13316552bd08
------ Level 3 | Size 1 | Label: 30
------ Level 3 | Size 1 | Label: 31
---- Level 2 | Size 3 | Label: bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb087989746776a8d3083a
------ Level 3 | Size 1 | Label: 32
------ Level 3 | Size 1 | Label: 33
Validation
As for valid and contains:
In [30]: merkle.valid(t)
Out[30]: True
In [36]: merkle.contains(t, b'4')
Out[36]: []
In [37]: hash_path = merkle.contains(t, b'3')
In [40]: for (h, maybe_left, maybe_right) in hash_path:
...: print(h.hex(), ' | ', maybe_left.hex() if maybe_left else None, ' | ', maybe_right.hex() if maybe_right else None)
...:
8dc28b40624872b5ef939e482f3ab934e30c074422ac38b81c6fffe1394571d648dba783236d6d69b8ea472121ea8f35616a8926ddcdb565c6e0b1c60852cce6 | 069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e13316552bd08 | bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb087989746776a8d3083a
bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb087989746776a8d3083a | 32 | 33
33 | None | None
… where the HashPathis as defined previously: a list of triples of the (node hash, left child hash, right child hash) from root to leaf. As we expect, it returns an empty list if the sought leaf does not exist.
Second Preimage Attack
Given the above tree, an attacker could try to trivially create a valid, shorter tree that features the same root hash. After all, the root is just the hash of its two children, whose values are known. (See also wikipedia example).
In [19]: h1 = bytes.fromhex('069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e133
...: 16552bd08')
In [20]: h2 = bytes.fromhex('bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb08798974677
...: 6a8d3083a')
In [25]: t2 = merkle.from_list([h1, h2])
In [26]: merkle.show(t2)
-- Level 1 | Size 3 | Label: 04f0c973b781a56ad3972609aaf8323572741f91a6104b7207ece6681fc44af83834136f7a1f2cb4078a5b3b11786bc815ab484b4d516e70b01769424ae47717
---- Level 2 | Size 1 | Label: 069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e13316552bd08
---- Level 2 | Size 1 | Label: bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb087989746776a8d3083a
Hmm… the root hash is different from our previous tree, so the trivial attack did not work. Why is that?
The MerkleTree implementation adds \x00 to leaf nodes and \x01 to interior hashes, thereby preventing the second preimage attack (at least for attacker using the given MerkleTree interface).
We can observe this by showing the prefixes:
In [27]: merkle.show(t2, show_prefix=True)
-- Level 1 | Size 3 | Label: 0104f0c973b781a56ad3972609aaf8323572741f91a6104b7207ece6681fc44af83834136f7a1f2cb4078a5b3b11786bc815ab484b4d516e70b01769424ae47717
---- Level 2 | Size 1 | Label: 00069616c3edf289c7d1a5fc11f6dc8fc0f9aabf64e43adda780803b23f871b4ad0bfa71996ac80bbb6fca433950e78d74cd82772802d67f7ffc4e13316552bd08
---- Level 2 | Size 1 | Label: 00bb839f4bf4a8199e293129964b903bd9e20f25558c8bc110238ce9eccf979843c5162655623ad85b38cea194b19b2cbbb7004d4910fb087989746776a8d3083a
And indeed, if we manually create a hash with the prefixes, we get the same root hash as before.
In [26]: hash.hash(b'\x01' + h1 + b'\x01' + h2).hex()
Out[26]: '8dc28b40624872b5ef939e482f3ab934e30c074422ac38b81c6fffe1394571d648dba783236d6d69b8ea472121ea8f35616a8926ddcdb565c6e0b1c60852cce6'
Tests
As always, it’s good to (at least) write some basic / base-case tests. In this case, constructing some small trees and testing for size, validity, etc is probably the minimum required.
Wrapping Up
The handling of Optional is a bit clunky in places (may be simpler to use a monadic fmap?), and the construcion and validation functions not being class methods may be a bit counterintuitive, but it seems to get the job done.
The implementation of contains is probably the most suboptimal, since it requires the entire tree to be walked. There is no way to not do this given the recursive tree implementation, but production blockchain nodes probably just store raw transactions and construct the specitic hash path as needed (rather than storing / walking the entire tree).